摘 要:分析强化学习课程教学中存在的问题,将“路径寻优”案例引入课程教学,探索以一个案例串联强化学习核心算法的教学方法。首先,基于“路径寻优”案例构建马尔可夫决策过程模型;其次,阐述动态规划方法、蒙特卡洛方法、时序差分方法的原理及区别;最后,结合“路径寻优”案例,通过关联编程,更加直观地讲解强化学习核心算法的区别,提高强化学习课程的教学质量。
强化学习是人工智能领域的核心内容之一[1]。2016年,以Alpha Go为代表的深度强化学习战胜了人类围棋冠军,成为人工智能领域又一个里程碑[2]。随后深度强化学习在人工智能领域取得越来越多的高水平成果[3,4,5]。自2018年4月教育部发布《高等学校人工智能创新行动计划》[6]以来,各高校积极建设人工智能课程体系[7],深度学习等机器学习课程建设得到了快速发展;与此同时,清华大学、南京大学、南开大学等高校陆续开设强化学习课程。然而,强化学习课程改革研究尚处于探索阶段,如何通过调整使其教学模式适应人工智能学科发展需要仍是一个重要问题。
由于强化学习理论较为抽象,需要较为宽广的知识储备,初学者往往难以掌握强化学习的核心思想,同时该课程还存在知识点零散及算法理论与代码脱节等问题,教学模式有待进一步完善。笔者将强化学习的理论教学与实践教学相结合,探索以一个实例串联强化学习核心算法理论的教学方法,旨在使学生更好地掌握强化学习的基本思想,培养学生运用人工智能算法理论解决实际问题的能力。
1 强化学习课程教学中存在的问题
1.1 学生知识储备不足
马尔可夫决策过程用于描述序贯决策问题,是强化学习的理论基础,诸多强化学习算法都是由动态规划方法演化而来的[8],但是部分学生并不具备上述理论知识。与此同时,强化学习需要一定的编程基础,这对该课程的入门学习造成了一定障碍,要求学生进一步提升知识储备。
1.2 知识点零散难统一
受AlphaGo里程碑事件的影响,各高校开始重视强化学习课程建设。强化学习理论体系自身仍在不断完善之中,而且知识点零散,难免会有部分教师对强化学习理论体系理解不到位,加之强化学习授课经验不足,缺少合适的教材,往往在课程讲授过程中不易找出一条主线串联强化学习理论体系。
1.3 算法理论与代码脱节
学生要想真正掌握强化学习课程的教学内容,除了要理解算法理论外,还要能够进行编程实践。强化学习算法理论与代码是相辅相成的,学生通过编程实践可进一步理解算法理论。然而由于课时等因素的制约,在当前强化学习课程教学中存在算法理论与代码脱节的问题。
针对上述三方面问题,结合强化学习教学实践,课题组提出以一个实例串联强化学习核心算法理论的教学方法,通过多次关联编程提升学生的编程能力,加深学生对算法理论的理解,激发学生的学习热情,从而改善强化学习课程的教学质量。
2“路径寻优”案例在强化学习课程教学中的实践
“路径寻优”案例在强化学习课程教学中可用10~14学时来完成。笔者在此介绍案例设计、核心算法及关联编程,旨在结合“路径寻优”案例,通过关联编程这一直观过程,降低教师的讲授难度,提高学生的接受程度,进一步加深学生对强化学习核心算法理论的理解。
2.1 案例设计
如图1所示,“路径寻优”案例选用一个4行4列网格,每个网格为一个状态,设定状态1是起点,状态16是终点,设定每个状态相应的奖励值并标记为不同的颜色。“路径寻优”任务的目标是寻找从起点到终点的最优路径,选用Python进行编程。
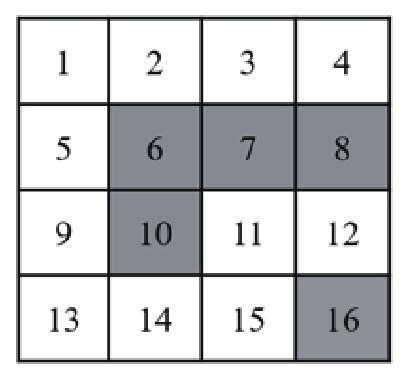
图1“路径寻优”案例
笔者针对“路径寻优”案例,构建马尔可夫决策过程模型如表1所示。
表1 马尔可夫决策过程模型

马尔可夫决策过程模型选用离散状态空间,包含16个状态;选用离散动作空间,包含上、下、左、右四个动作,智能体执行动作后若跳出网格则仍然返回原状态。状态所对应奖励值用不同颜色标记,白色代表状态奖励值为-1,绿色代表状态奖励值为-10,终点标记为黄色且奖励值为100。
结合“路径寻优”案例,笔者在所构建的马尔可夫决策过程模型基础之上,分别讲授动态规划、蒙特卡洛、时序差分三类强化学习核心算法理论,然后引导学生结合相应算法理论进行编程,最终得到最优路径,如图2所示。
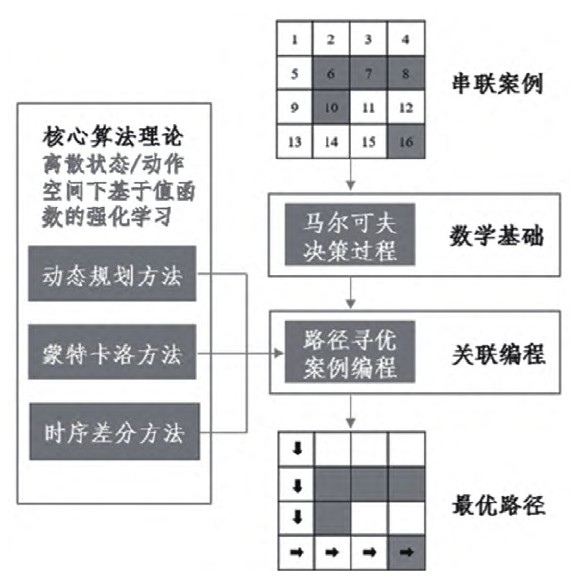
在课程讲授过程中,教师针对所引入的“路径寻优”案例,有目的性地补充数学基础和编程知识,可以解决学生知识储备不足的问题。结合“路径寻优”案例,着重对比不同算法在理论及代码方面的区别,通过同一个案例将强化学习核心算法进行串联,有效解决知识点零散难统一的问题。此外,通过同一个案例在不同算法中的多次编程,可以更加直观地讲授强化学习核心算法的基本原理,从而提高教学质量。
2.2 算法理论
强化学习是一个与时间相关的序列决策问题,智能体与环境在每个时间步进行交互,先观察当前所处状态,根据强化学习算法采取相应动作,接着智能体进入下一个状态并观测所对应的奖励值,依次进行策略评估和策略改进,最终找到最优策略[8]。面向离散状态/动作空间,以基于值函数的三类强化学习算法为例,笔者提出采用一个“路径寻优”实例进行串联讲解的教学方法。三类算法理论及区别介绍如下。
2.2.1 动态规划方法
该方法是指在给定一个马尔可夫决策过程描述的完备环境模型下,动态规划使用价值函数来结构化地组织对最优策略的搜索,在每个时间步采用贝尔曼最优方程计算价值函数值,通过策略评估和策略改进两个步骤不断迭代得到最优策略。传统动态规划需要遍历全状态空间,而异步动态规划可跳过与最优行为无关的状态,从而提升效率。
2.2.2 蒙特卡洛方法
与动态规划方法一致,蒙特卡洛方法包括策略评估和策略改进两个方面。而与动态规划方法不同的是,蒙特卡洛方法不需要完备模型。蒙特卡洛法方法学习状态价值函数是利用经验平均代替随机变量的期望,对所有经过这个状态之后产生的回报计算平均值,采样越充分,平均值就会越收敛于期望值。因此,蒙特卡洛方法是在完整的一幕结束后才能进行策略评估和策略改进,而非在每个时间步进行。
2.2.3 时序差分方法
时序差分方法是强化学习的核心算法。与蒙特卡洛方法一致,时序差分方法不需要完备模型,而是在与环境交互中学习。与动态规划方法一致,时序差分方法可在每个时间步对值函数进行策略评估和策略改进,而非在完整的一幕结束后。若多步时序差分方法将值函数计算步数不断扩大则最终会成为蒙特卡洛方法。
2.3 关联编程
学生在“路径寻优”案例构建的马尔可夫决策过程模型基础之上,根据三类强化学习算法理论,以更加直观的方式进行编程。由于采用同一案例对三类算法进行编程,代码会有多次重复和关联,仅决策代码有所区别,因此,可以通过关联编程更加直观地展示算法的区别。
三类强化学习算法在编程上最显著的区别是值函数更新的方式不同。如图3所示,空心圆为状态,实心圆为动作,st为初始状态,rt+1为奖励值,st+1为下一个状态,send为终止状态。时序差分方法仅需要对t和t+1两个时间步进行采样就可以更新值函数,蒙特卡洛方法需要采样到一幕的终止状态才能更新值函数,而动态规划方法则需要遍历全部状态空间才可以更新值函数。因此,可以根据伪代码,结合图3中的不同值函数更新方法,对三类强化学习算法进行关联编程。
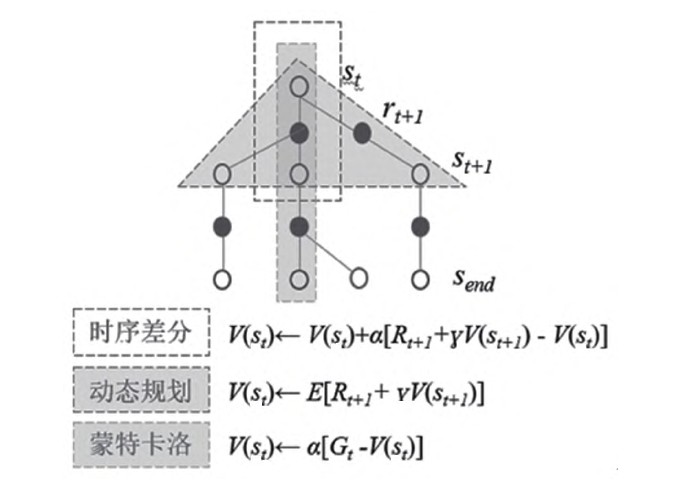
在以往的教学中,学生容易混淆上述三类强化学习算法理论。笔者在教学过程中引入“路径寻优”案例,通过比较三种算法在同一个案例编程方面的区别,直观讲授三种算法的不同,降低教师的讲授难度,提升学生的接受程度,从而解决算法理论与代码脱节的问题,提高强化学习课程的教学质量。
3 结语
本文阐述了在强化学习课程教学中引入“路径寻优”案例,通过一个案例串联强化学习核心算法理论的教学方法。案例简单明了,通过讲授算法理论及其区别,结合同一个案例在不同算法中的多次关联编程,学生可以更加直观地学习强化学习算法理论,有效改善强化学习课程的教学质量。
参考文献
[1]WANG H N, LIU N, ZHANG Y Y, et al. Deep reinforcement learning:a survey[J]. Frontiers of Information Technology&Electronic Engineering, 2020(21):1726-1744.
[2]SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature,2016, 529(7587):484-489.
[3]SCHRITTWIESER J, ANTONOGLOU I, HUBERT T, et al.Mastering Atari, Go, chess and shogi by planning with a learned model[J]. Nature, 2020(588):604-609.
[4]DEGRAVE J, FELICI F, BUCHLI J, et al. Magnetic control of tokamak plasmas through deep reinforcement learning[J]. Nature,2022(602):414-419.
[5]FAWZI A, BALOG M, HUANG A, et al. Discovering faster matrix multiplication algorithms with reinforcement learning[J].Nature, 2022(610):47-53.
[6]秦记峰,任东海.人工智能课程实践教学改革探讨和研究[J].计算机教育,2019(10):12-15.
[7]教育部.关于印发《高等学校人工智能创新行动计划》的通知[EB/OL].http://www.moe.gov.cn/srcsite/A16/s7062/201804/t20180410_332722.html.
[8]SUTTON R S, BARTO A G. Reinforcement Learning:An Introduction[M]. MIT Press, 1998.